みずほリサーチ&テクノロジーズ サイエンスソリューション部上席主任コンサルタント 宇野 隼平
―近年、量子コンピュータを取り巻く環境は大きく変化している。
最前線で研究を進める研究者は、今の世界をどう見て、未来をどう作り上げていくのか。本連載では、日本で量子コンピュータ技術の研究開発において活躍する若手研究者の声から、量子コンピュータにまつわる様々な視点を届けていく。
量子コンピュータの社会実装が早いのは、金融分野だと指摘する声は多い。例えば、デリバティブ（金融派生）商品の価格決定時に行うモンテカルロシミュレーション。現在のコンピュータでは、デリバティブ商品の価格決定に際し、当日の株式市場が締まったあとに、計算をはじめても、結果を知るには日を跨がねばならない。一方で、まだまだ量子コンピュータは、ノイジーで、ビット数も少なく理想のマシンとはなっていない。そこで、ノイズが不可避、ビット数の少ない現在の量子実機、NISQ（Noisy Intermediate-Scale Quantum）デバイスを使い、デリバティブの価格決定計算等を通じて、量子コンピュータを高速化するアルゴリズムを研究しているのがみずほリサーチ＆テクノロジーズの宇野隼平氏だ。今回、NISQデバイスをどう活用するのか、また、今後の理想的な量子コンピュータにどう対応するのかを伺った。
（聞き手・構成・写真：増山弘之）
宇野 隼平（うの・しゅんぺい）
みずほリサーチ&テクノロジーズ サイエンスソリューション部上席主任コンサルタント
慶應義塾大学 量子コンピューティングセンター 共同研究員
2011年3月 名古屋大学大学院理学研究科・博士後期課程修了。専門は素粒子理論。
2011年4月 みずほ情報総研株式会社(現：みずほリサーチ&テクノロジーズ)に入社し、確率論的破壊力学、流体・構造連成解析等の物理シミュレーションに携わる。
2015年4月～2017年3月 日本原子力研究開発機構に出向
2018年5月よりIBM Quantum Network Hub @ Keio Universityの研究者として、金融業務における量子コンピュータの活用に向けた研究活動に従事。
発祥は、富士銀行グループの芙蓉情報センターの時代に遡ります。その中に科学技術にかかる計算に特化していた専門組織があり、この部門の資産を引き継いでいるのが私たちサイエンスソリューション部です。なので50年以上の歴史があります。業務としては、得意分野の高度な計算技術を活用し、科学技術領域のコンピュータシミュレーションと調査を行っています。官公庁系、民間系の課題解決が半々で、部員数は約60名。ほぼ全てのメンバーが修士や博士を持つ専門家集団となっています。
これまで私は、原子力プラント内で起こる様々な現象のシミュレーション等、金融分野からは少し遠い領域で活動してきました。今回は、金融機関、みずほフィナンシャルグループとしての課題に直結する金融領域での研究を進めています。
2018年5月に慶應義塾大学 量子コンピューティングセンター内にIBM Quantum Network Hub @ KeioUniversity (略称QHuB）が開設され、7月に共同研究員として参画しました。第1期が2020年で終了し、2021年から第２期がスタートしたところです。当社としても、企業から人が常駐して行う、あまり前例のない産学連携のスタイルとなっています。みずほフィナンシャルグループとしては、フィンテック領域のイノベーションが進む中、新たな技術を積極的に取り入れて、新しいことをやらないといけないという問題意識があります。重点分野の例としては、AＩ、IoT、ブロックチェーン、そして量子コンピュータといったものが挙げられます。
科学技術系の数理モデル領域に手広く関わりたいと思ったからです。大学では細い分野に特化せざるをえず、どうしても数値計算を学んだことを活かせる幅が狭いのです。一方、企業の研究所だとかなりプロダクトに寄った研究になるので、これまた分野が限られる。科学技術計算を幅広くできるというと、他に選択肢もなく今の会社での研究職を選びました。
そして、コンピュータによる計算に興味をもったのは、博士課程の研究が素粒子であったことと深く関係しています。素粒子理論は、物質が何から出来ているかを、還元論的に調べていく分野なのですが、特に私は量子性の強い複雑な現象に興味があったため、自ずからコンピュータによるシミュレーションが必要となってきました。
そもそもなぜ、素粒子だったのかというと、根源的な宇宙の原理を知りたかった。自分がどこから来て、その自分は何から出来ているのか、といったことを解明していきたいという思いがありました。
大きく分けると、金融における攻めの分野である、「価格のシミュレーション」、「機械学習によるリスク評価」、「ポートフォリオの最適化」などがあり、守りの分野では「量子コンピュータで今の暗号はいつまで持つのか（危殆化問題）」といった研究があります。特に、これまでは価格のシミュレーションに力を入れており、量子コンピュータを使ってデリバティブ商品の精緻な価格評価をどう行うのかといった研究を行ってきました。
デリバティブ商品の価格決定は、一般的にはモンテカルロ法によって乱数を発生させ、できるだけ多くの価格変動シナリオをシミュレーションして行います。適性価格はその平均値を計算することで導き出します。
たとえば、ある企業の株を1年後に一株あたり1,000円で買える権利（コール・オプション）を（売り手の金融機関として）今、いくらで売れば良いかという計算を行います。できるだけ沢山のシナリオを発生させたほうが、より精度の高い価格決定ができるわけですが、現状ではデリバティブの価格決定には数時間以上コンピュータを動かす必要があります。これを短くしたいというのが金融業界の要請です。
今、コンピュータクラスタで計算するにしても、証券取引所のその日の場が締まってから計算を始め、翌日朝に結果が知れるという状況になっています。もし量子コンピュータによる高速化が行われれば、場が締まったその日のうちに価格決定ができるだけでなく、もしかしたらリアルタイムで状況を反映出来るようになるかもしれません。このようにモンテカルロシミュレーションの高速化は金融機関にとって重要な課題の一つであり、私たちだけでなく、JPMorgan Chase、Barclays、Goldman Sachs、BMO、Scotiabank等の金融機関も量子コンピュータを使って研究を進めている状況です。
分かりやすく言えば、古典コンピュータでは、価格変動のシナリオ１、２、３・・・と一つずつ計算せねばなりませんが、量子コンピュータであれば、量子の重ね合わせによって、多くのシナリオが同時的に探索できる。これにより、将来の様々な価格変動を正確にシミュレーションして、現在の金融商品の価格を決定するわけですが、理論上はモンテカルロ計算が2乗加速できるのです。
その通りで、現時点ではノイズのない理想の量子コンピュータは存在せずNISQデバイスを活用するしかありません。しかし、古典計算機に対して優位性を持つようなNISQアルゴリズム、例えばGoogleの量子超越性を達成したコンピュータでは高速化するアルゴリズムはあるものの、何の役にたつかわからない。そこで、何らかの適応可能なアプリケーションを探索しなければならないという研究課題があります。
一方で、未だ速度向上がどれくらいできるのかが不明瞭なNISQアルゴリズムもあり、科学計算、最適化、機械学習といったアプリケーションは提案されているものの、実際にアルゴリズムを使って本当に速度が向上するのか実機を使って確認していく必要があるという課題もあります。
私の場合は、こういったNISQの課題に取り組みつつも、さらに速度向上が確実な理想的な量子コンピュータに使えるアルゴリズムを先行的に開発するという研究を行っています。具体的には、慶應義塾大学からアクセスできるIBMのNISQ実機を利用した経験を活かして、アルゴリズムや数理モデルを作り、「できるだけ少ないビット数」で、「できるだけ多くの演算数」を実現し、なおかつそれを「ノイズの制約下で効率的」に実現できるかという課題に取り組んでいます。
現に、アルゴリズムの紹介サイトQuantum Algorithm Zoo（https://www.qmedia.jp/algorithm-zoo/）によると、ノイズのない理想の量子コンピュータであれば、速度向上が可能なアルゴリズムは現在50個くらい提案されています。これらは理想的なコンピュータでないと動かないものが多いので、各アルゴリズムがノイズに対して強いか弱いかの検証が必要なのです。
一方でNISQデバイスを使うとすると、NISQの性能による制限があります。今日では、メモリが最大値で数十量子ビット。ここ数年で数千量子ビットに到達できるかどうかという状況です。今の古典コンピュータでは100万ギガ、100万ビットが使えるわけなので、古典コンピュータに比べると非常に小さいメモリです。また、演算数も限られていて、量子状態が壊れる前に、計算を終える必要があります。結果がノイズまみれになるので、そこから有効な信号を取り出す必要がある。このような課題をどう解決するかという研究をしてきました。
通常の量子コンピュータの使用方法であれば、各計算を逐次的に行い、途中で計算するための補助ビットが必要となります。今回の提案手法では、量子計算が得意な部分のみを、量子コンピュータで分割、並列的に計算し、量子計算の結果を古典コンピュータで統計します。分割単位をそれぞれ個別に計算することで、補助ビットも減らせノイズの影響も減らせるのです。
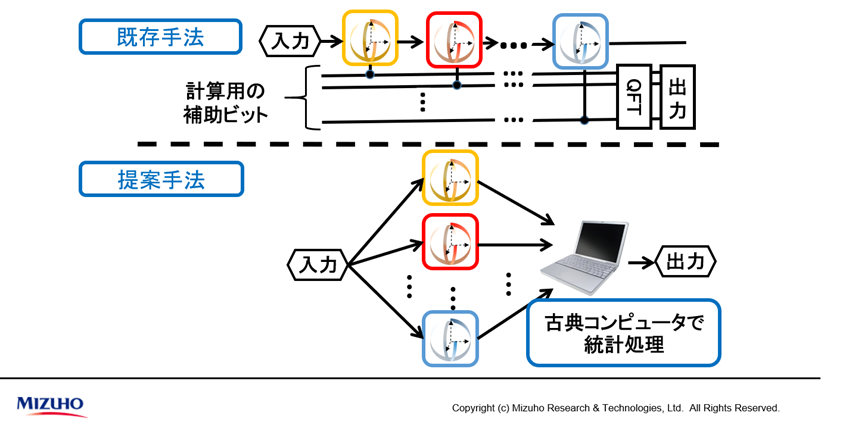
これにより、既存の量子アルゴリズムを適用しつつも、1回の計算にかかるビットの演算数をそれほど増やすことなく計算できるということが分かりました。次の左図にあるように、横軸がサンプル数（＝シナリオ数）を表しており、通常はサンプル数が増えると演算回数が増える（グラフ青線）ものですが、提案手法では、サンプル数が増えても、演算数は1/20程度に抑えられる（グラフ赤線）ことが分かりました。
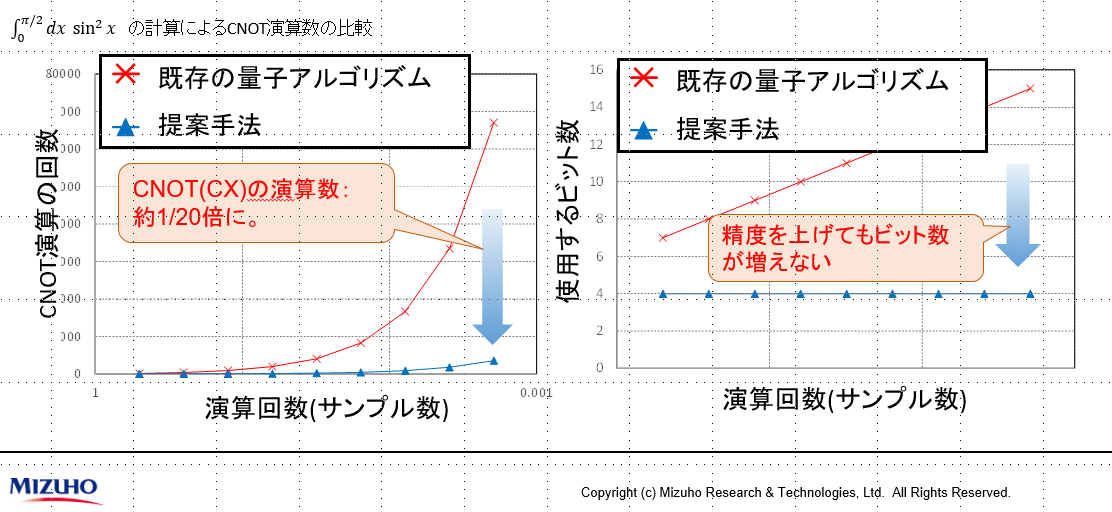
また、右図では、演算の精度を上げてもビット数を抑えられるということを示しています。つまり、逐次計算であれば、演算の精度を上げると補助ビット数が増えていきますが、この手法であれば、既存の量子アルゴリズムでも、ビット数を増やさず対応できるということです。
この実験は、実用面だけでなく、学術的にも興味深い結果となりました。ニールセン＝チャンの有名な教科書「量子コンピュータと量子通信〈1〉量子力学とコンピュータ科学 (量子コンピュータと量子通信 1)」の中に、アルゴリズムを説明する章があります。その1ページ目に次のような図が出てきます。
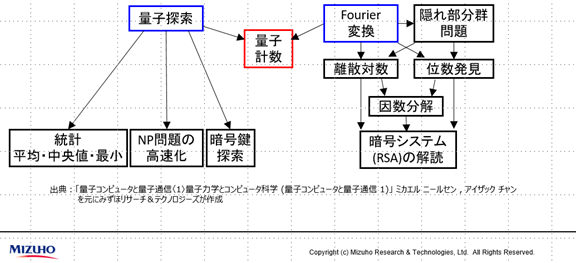
図によると、ほとんどの量子コンピュータのアルゴリズムは量子探索とFourier変換のアルゴリズムという２つから派生しており、モンテカルロ法はこれらを両方使わないと、量子計数が出せない珍しいケースとされている方法です。
今回、改良した方法では、量子計数は量子探索のみで算出可能であることを実証しました。つまり、今回この教科書を書き換えるような成果が出たということですね。
以上のようにして、ビット数と演算数の２つの課題に対応しました。
次はノイズの課題です。もしノイズが無ければ量子コンピュータで計算を行っても、演算数の増加にともなう量子の振動数は変わりません。以下の左図のようにオレンジ線のサインカーブのようになります(量子計数はこの振動数を推定することでモンテカルロ計算を行う)。
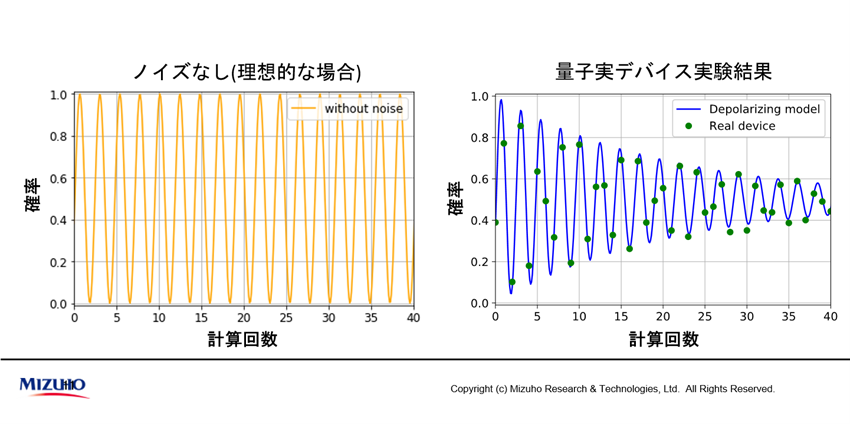
ところが、実機での計算結果は右図の緑点に現れます。現実にはノイズにより、振動数が減衰していくことになるのです。そこでノイズの中から信号(振動数)を推定する方法を考案しました。
これにより、ノイズの有り無しによってどの程度モンテカルロ法のパフォーマンスに影響が出るのかというシミュレーションができるようになりました。この方法によって、ノイズがある場合の計算精度の理論曲線を導出し、どの程度ノイズが減少すれば、古典コンピュータを上回ることが出来るのかを推定できました。
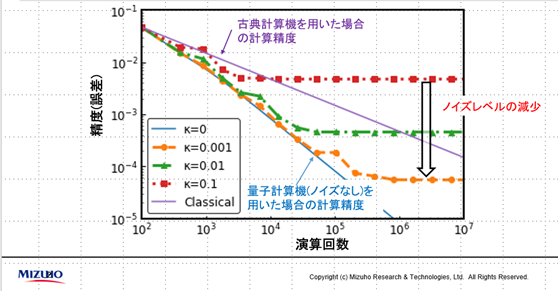
この理論値が正しいかどうかは、やはり実機で検証する必要があります。
果たして、実機を動かしてみると、実際に、古典コンピュータより精度高く計算できることを確認(同じ演算回数の場合)することができました。ただ、実証では理論値と測定値が合致しすぎてしまい、かえって怪しいなと思い何度も検証することとなりました。何度計算しても、やはり合っていたのですが…。
これにより、当初の課題はクリアし、「ビット数」、「演算数」、「ノイズの影響」に対応したわけですが、もっとよい方法はないかと探求しました。
ノイズの下での精度の限界は存在するのか？という問いに対し、別の手法でノイズがある場合の計算精度の限界を導出することができました。詳細は省きますが、計算精度の限界に近い精度を達成できるような、新たなアルゴリズムも考案しており、現在特許を申請中です。
今回の結果は論文ベースでは、以下の3本にまとめることができました。
Amplitude estimation without phase estimation(2019/04)
Amplitude estimation via maximum likelihood on noisy quantum computer(2020/06)
Modified Grover operator for amplitude estimation(2020/10)
現在の研究は、金融機関としての具体的な計算ニーズから出てきているものとはいえ、今まではどちらかと言えば基礎的な研究をやってきました。今後は、それをさらに掘り下げるとともに、もっと他の応用に近い研究にも取り組んでいきたいと考えています。
さらに、その後は金融以外でも、数理モデルを広く活用したいと考えています。ニーズが顕在化している領域だけでなく、量子コンピュータの出現によって、今まで不可能だった計算が可能になることで、数理モデルで新たにアタックできるような問題領域も射程に入るようになりました。言わばシーズドリブンで開拓できる分野も大きな可能性があり、是非追究して行きたいと考えています。
Q Hubは、教員、学生だけでなく企業の研究者も参画する産学連携の共同研究体となっています。同業では、三菱UFJ銀行さんや、三井住友信託銀行さんとも、机を並べて仕事をしており、現場の業務ではなかなかあり得ないことです。もちろん、金融だけでなく、化学や電機メーカーなどの企業さんとも、色々なアイデアについて気軽に雑談できるような環境です。議論しながら、各社とも野心的に量子コンピュータを何とか使ってやろうと取り組んでいます。多様性があって非常に良い雰囲気で、上手くコラボレーションができていると思います。
量子人材の不足が課題となっていますが、今後ますます、量子コンピュータの応用探索を行うニーズが高まってきます。それに際してコンピュータを実用化して行くためには企業の協力が欠かせません。研究と応用は、もともと領域の違う世界ですが、現在の量子コンピュータに対して何が不足しているかというと、泥臭いエンジニアリングなのです。研究者だけでなくて、今後は企業の協力がますます必要になってくるでしょう。
現在の私の研究は量子コンピュータでモンテカルロの計算スピードを上げたいという企業側の要求と、ノイジーなコンピュータの課題を解決したいという研究課題の現実的な折り合いから生まれたものです。したがって企業としては、各社の経営課題において、エンジニアリングで解決しないといけない新しい観点を入れて研究に参画するのがよいかと思います。
現状、Q Hubにおいても、量子に寄っているか、ドメインスペシフィックな事業領域に寄っているかで、量子と応用研究に両方に興味をもっている人材は少ないのですが、多様な人達と共同研究していくと研究の幅もひろがって、応用が進んでいくのかなと思います。量子だけやりたいという人は金融機関にはそもそも来ないと思いますが、金融の応用課題を量子で解決したいという人は今後出てくるのではないかと思います。そういった機会を増やし、少しでも業界に貢献できればと思い日々研究活動に取り組んでいます。
